miércoles, 12 de agosto de 2015
Calculando V.I
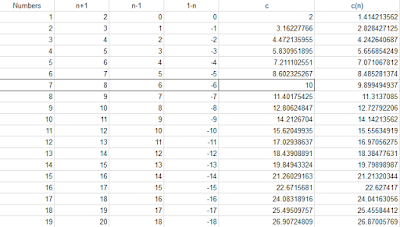
Después de más de 20.000 números usando lo del otro día, solo hay algunos que dan un número entero al calcular c usando el anterior y posterior como a/b en base al teorema de pitágoras:
- Empezamos por el 1, calculamos el anterior y el posterior:
n+1 = 2
n-1 = 0
- Sacamos la c, en base al anterior y al posterior:
c = 2
- Sacamos la c en base a 1:
c (1) = 1,4142135623730950488016887242097
- Repetimos el proceso con los otros números:
- 7:
n+1 = 8
n-1 = 6
c = 10
c (7) = 9,8994949366116653416118210694679
- 41:
n+1 = 42
n-1 = 40
c = 58
c (41) = 57,982756057296897000869237692598
- 239:
n+1 = 240
n-1 = 238
c = 338
c (239) = 337,99704140716971666360360508612
- 1393:
n+1 = 1394
n-1 = 1392
c = 1970
c (1393) = 1969,9994923857214029807523928241
- 8119:
n+1 =8120
n-1 = 8118
c = 11482
c (8119) = 11481,999912907158701220910751859
- 47321:
n+1 = 47322
n-1 = 47320
c= 66922
c (47321) = 66921,999985057230804344712118327
El siguiente número debería estar dentro del rango 5-5.86 teníendo en cuenta todos los saltos, está ampliado por si acaso y aún así no aparece, lo que me lleva a pensar que sólo hay 7, los cuales son 3 primos, 3 que no y el 1. Podríamos debatir sobre que es el 1 y en que grupo meterlo, a parte de ser diferente la c(n) con respecto al resto, todos los números son divisibles por él, lo cual hace que no necesite grupo en sí, etc. etc.
- Lo pasamos a una matriz y sacamos el determinante:
7 1 1393
41 1 8119
239 1 47321
det(A) = -1120
Suscribirse a:
Enviar comentarios (Atom)
No hay comentarios:
Publicar un comentario